About me

I am currently a final year PhD student at the University of Cambridge. In Cambridge, I am affiliated with the Department of Applied Mathematics and Theoretical Physics (DAMTP). In Oxford, I am a Recognised Visiting Student at the Mathematical Institute, where my PhD supervisor is, Maria Bruna.

Research

I am interested in mathematically understanding the emergence of collective behaviour. Examples of this emergent behaviour are lane formation in groups of ants or pedestrians, or flocking in birds.

Street crossing in Tokyo

I specialize in studying these phenomena using

• Stochastic differential equations (SDEs) and
• Partial differential equations (PDEs).

Schematically, I consider \(\mathbb{R}\)-valued systems of SDEs which can be written as $$ \mathrm{d}\mathbf{X}^{i,N}_t=\mathbf{b}^N(\mathbf{X}^{i,N}_t,\mathbf{X}_t^N)\mathrm{d} t+\sqrt{2}\mathrm{d}\mathbf{W}_t^{i,N}, \ i=1,\dots,N $$ for some drift function \(\mathbf{b}^N\). In the mean-field limit the \(k\)-marginals of the law, \(f^{(k)}_t(t,(\mathbf{x}_i)_i)\), converge to a tensorised product of \(f(t,\mathbf{x})\), in some \(d\)-metric topology, for any \(k\), $$ d(f^{(k)}_t,f(t)^{\otimes k})\to 0 \ \mathrm{as} \ N\to\infty.$$ In general, this needs to be proven for the specific modelling choice for the drift function \(\mathbf{b}^N\). The limit density \(f\) is a solution of the mean-field limit PDE and is, in this case, of the form $$ \partial_t f=\nabla\cdot[\nabla f-\mathbf{b} f],$$ if the limit \(\mathbf{b}=\lim_{N\to\infty} \mathbf{b}^N\) exists.

With this way that SDEs and PDEs describe collective behaviour in mind, I focus on

• PDE analysis (well-posedness, (non)linear stability, bifurcations),
• Developing numerical PDE and SDE schemes,
• Numerical analysis of these schemes,
• Rigorous mean-field limits,
• SDE parameter inference from data.

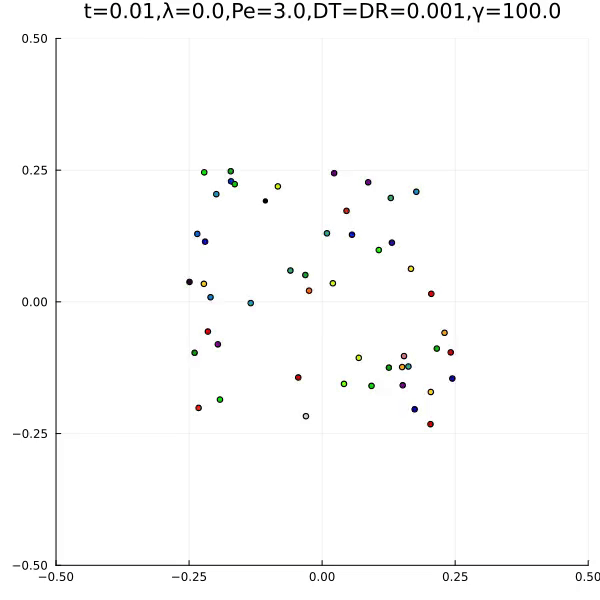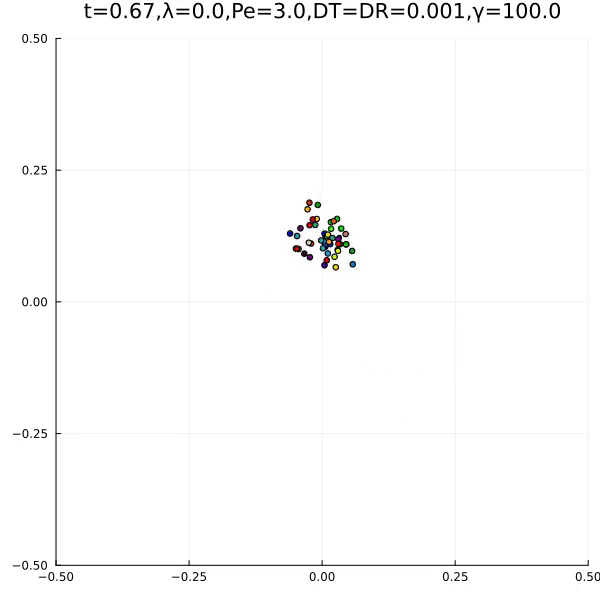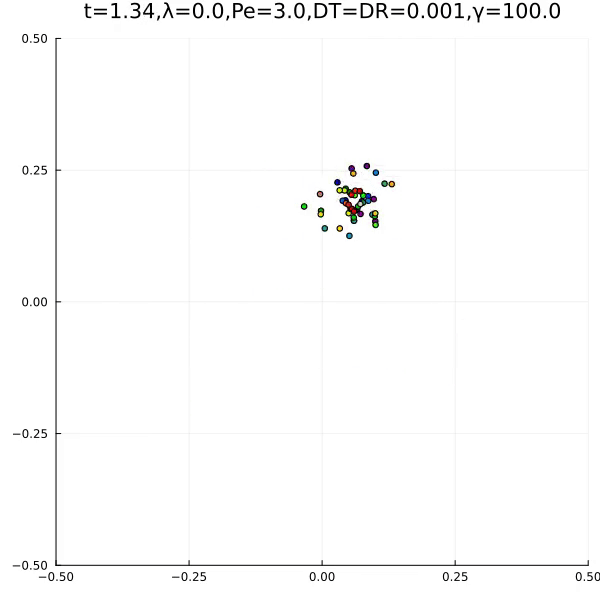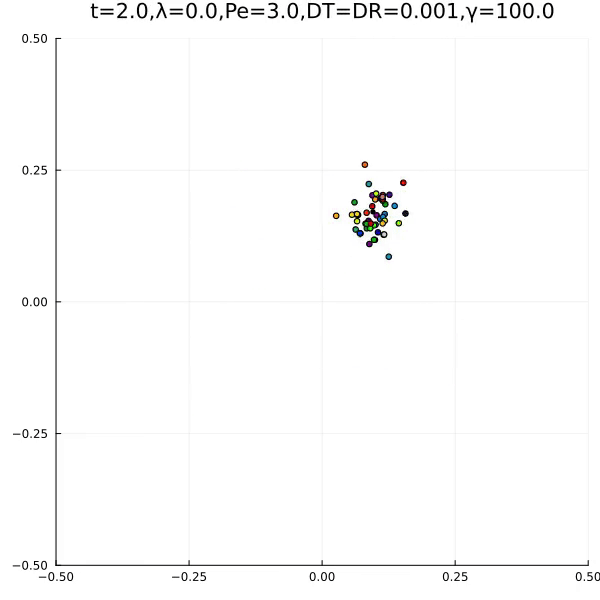
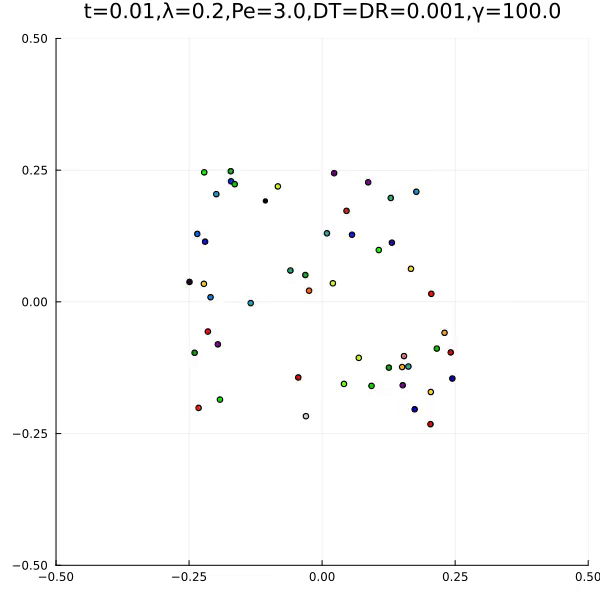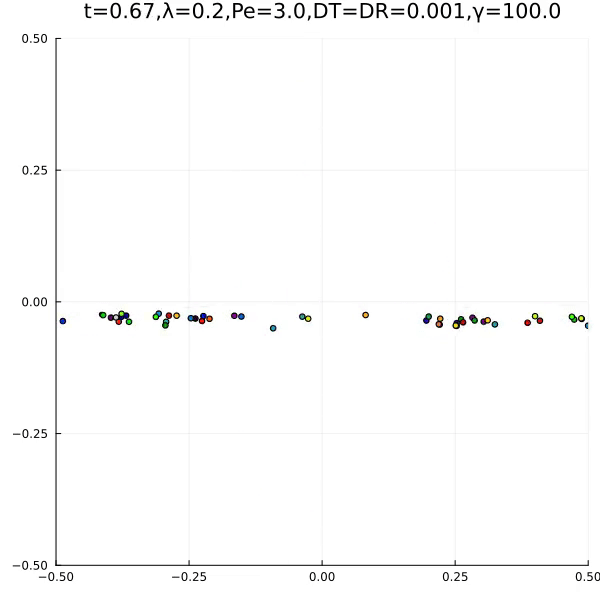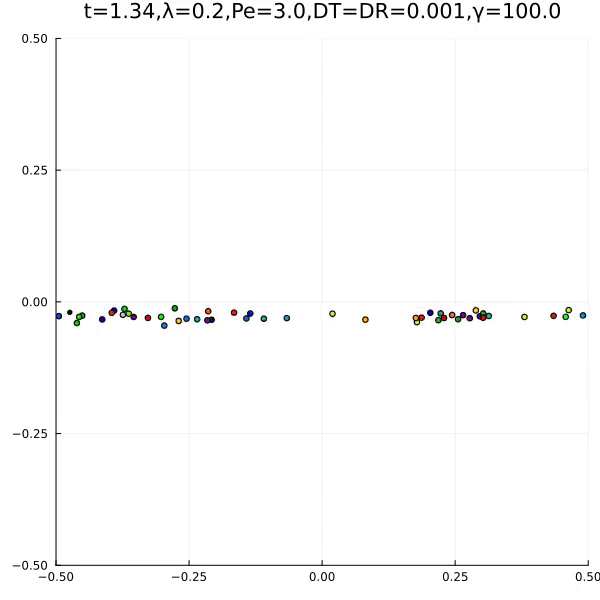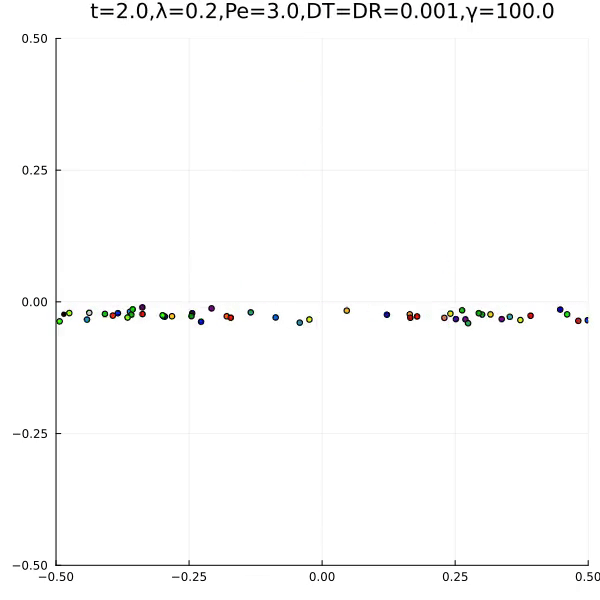
The first is an aggregation type behaviour. The second is the formation of a traveling cluster. In the paper we explain how this is related to lane formation and ant antennas.

An interesting feature of the PDE for our ant model, and of many other PDEs used to study models of so-called active matter such as groups of ants, birds and pedestrians, is that the PDE is different from a particular class of PDEs for which a substantial level of understanding has been achieved. This is the class of PDEs that can be written in the form $$ \partial_t f=\nabla\cdot\left(f\nabla\frac{\delta\mathcal{F}}{\delta\mathcal{f}}\right),$$ where \(\mathcal{F}\) is a functional of \(f\). These are PDEs that can be described as a gradient flow and the functional \(\mathcal{F}\) can be used to describe the PDE dynamics via a LaSalle Invariance Principle (see, for example, this paper).

In our case, for active matter PDE models, the PDE cannot be of this form, because the curl of the drift function \(\mathbf{b}\) is non-zero in our model. To give an example of how gradient flow dynamics can be different from a model that is not of the above form, we can consider the following two linear models. The first model has a mean-field limit PDE of the form $$ \partial_t f=\nabla\cdot[\nabla f-\nabla V f], $$ where we have exponential relaxation to the unique normalised steady state \(f_\infty(\mathbf{x})=\frac{1}{\int\mathrm{e}^V\mathrm{d}x}\mathrm{e}^{V(\mathbf{x})}\) for some potential \(V(\mathbf{x})\), and the second model is $$ \partial_t f=\nabla\cdot[\nabla f-(\nabla V+ \mathbf{U})f], $$ such that the perturbation \(\mathbf{U}\) satisfies \(\nabla\cdot\mathbf{U}=0\) and \(\mathbf{U}\perp\nabla V\), so that the steady state is preserved. The typical particle behaviour for these models is quite different. In the below videos, the grey background hue is the amplitude of the steady state potential \(V(\mathbf{x})\).

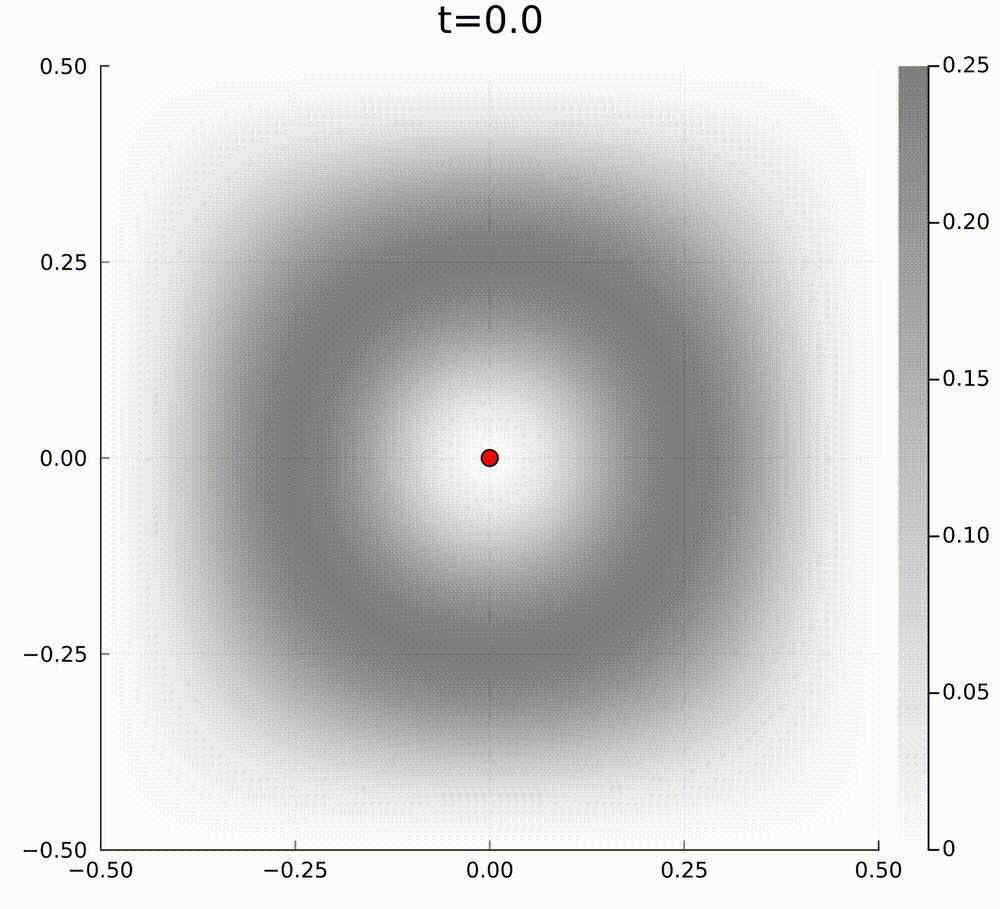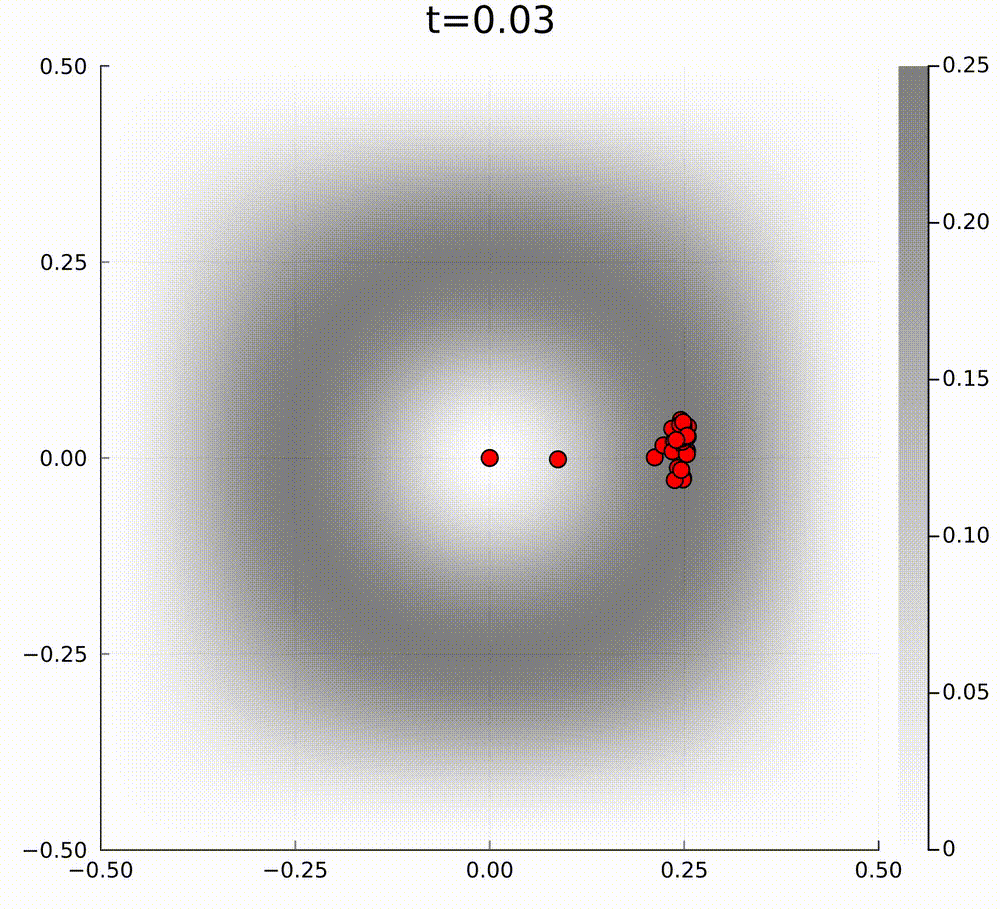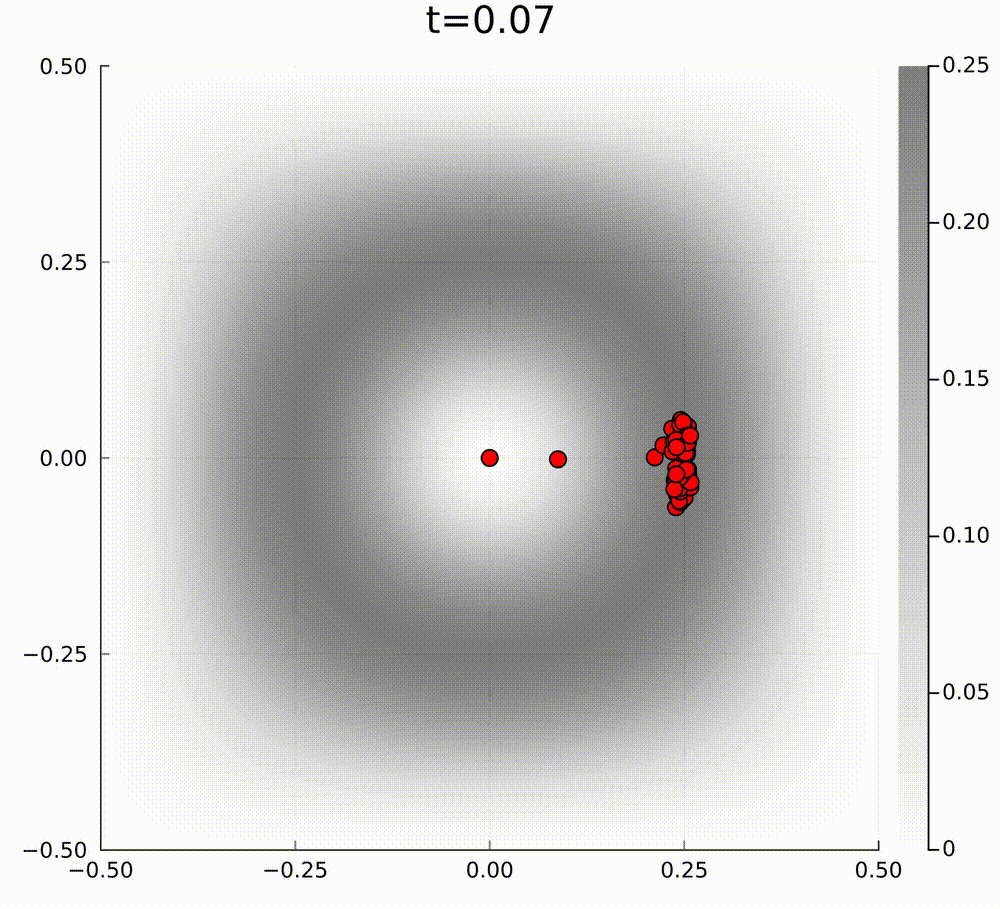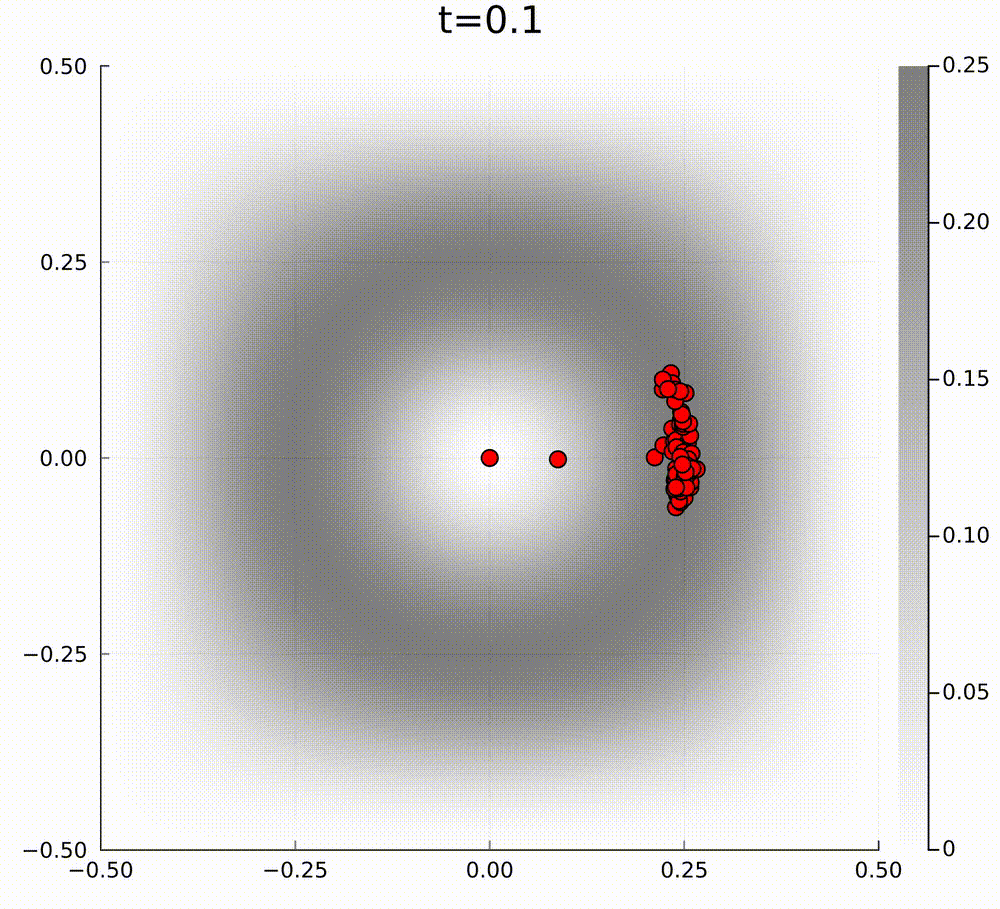
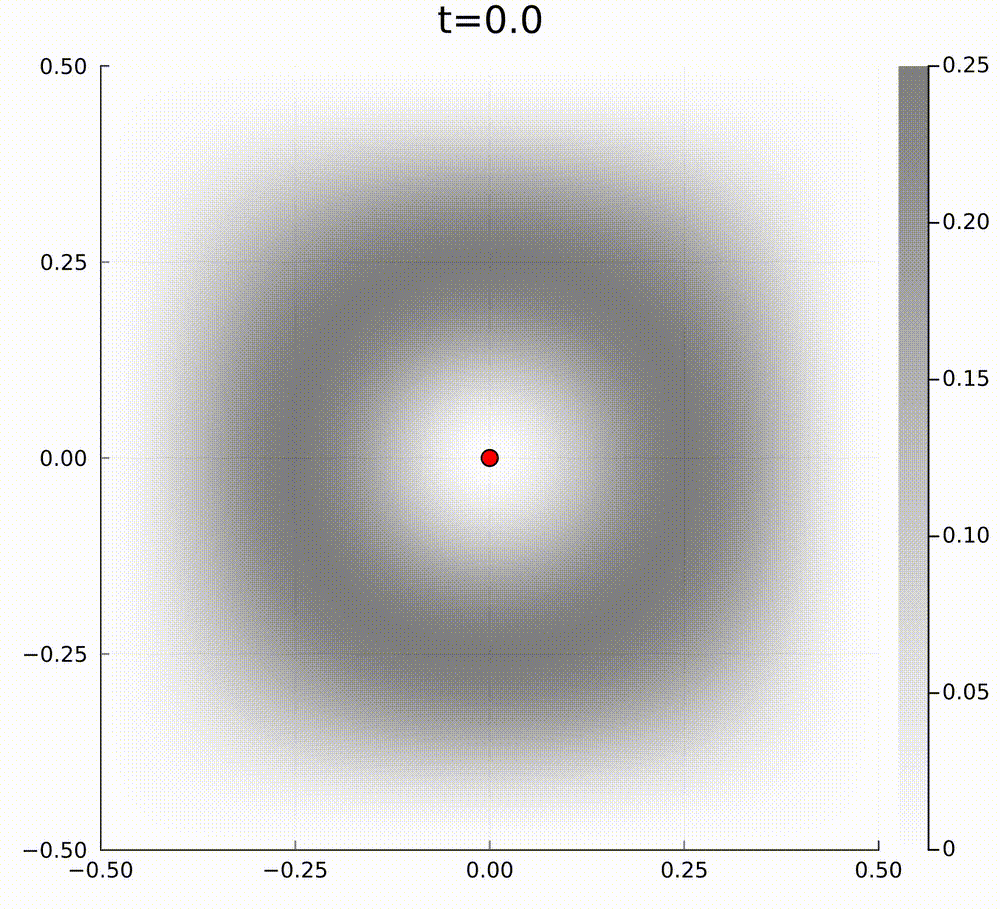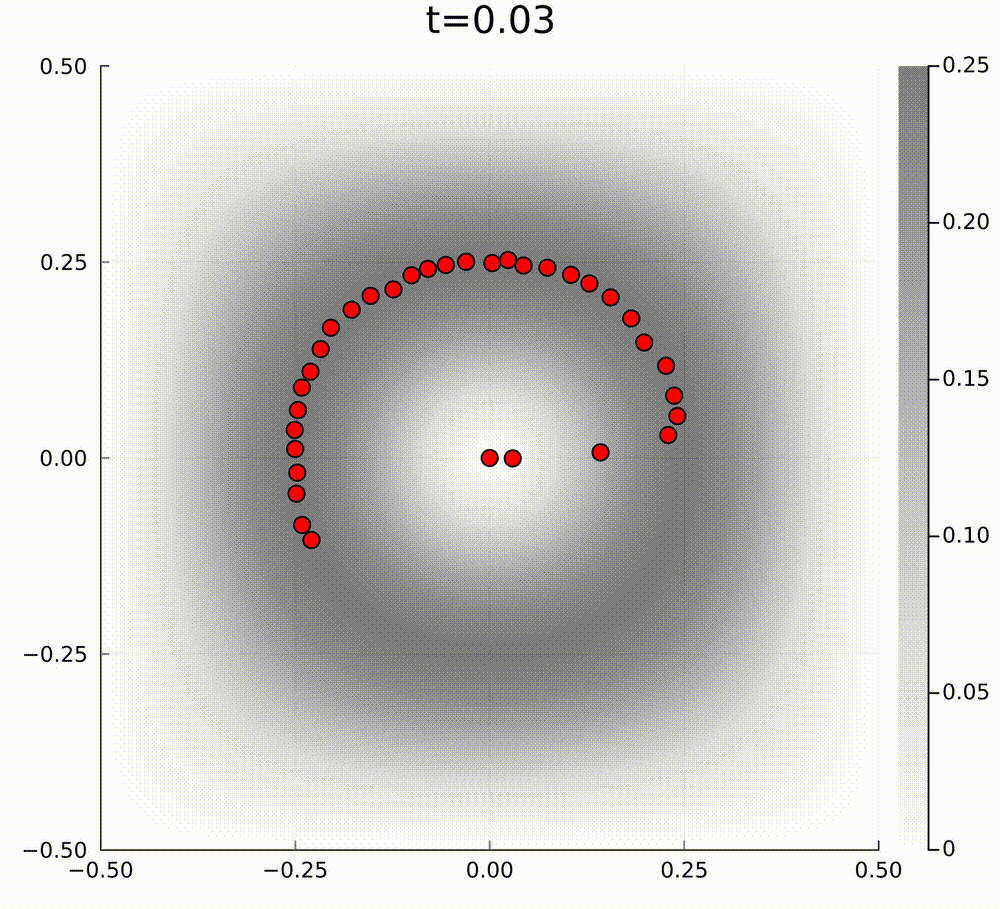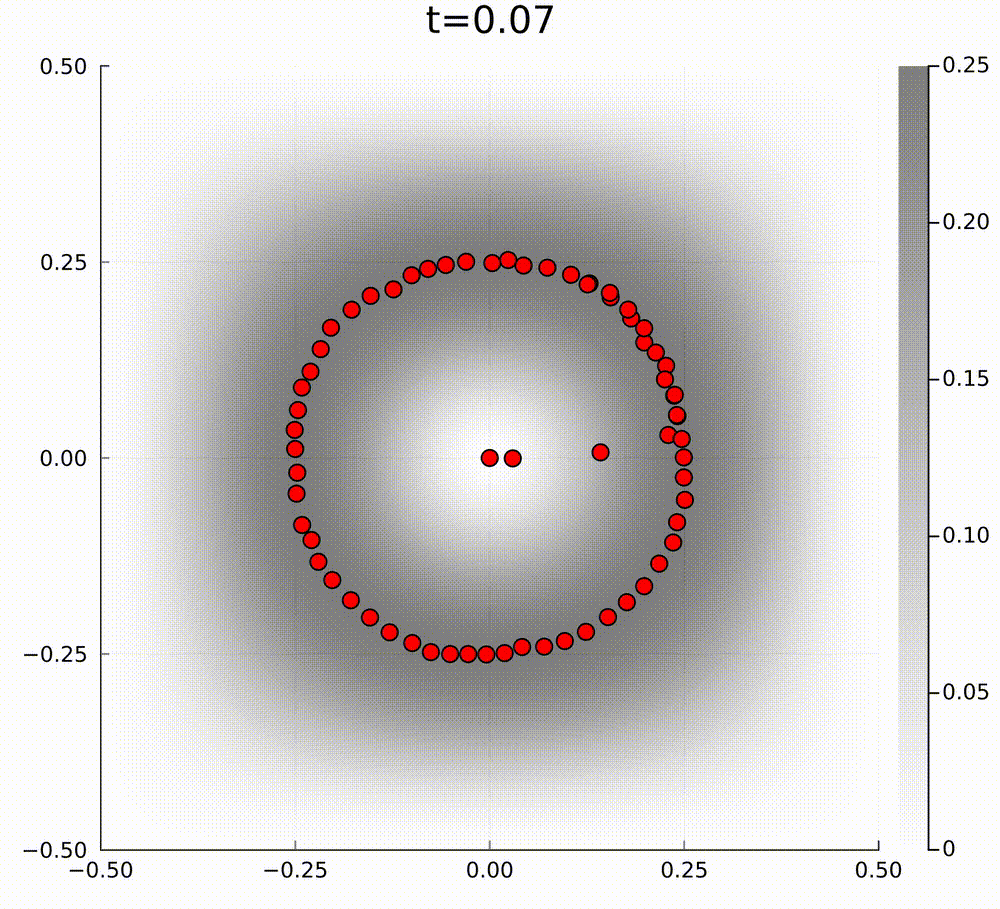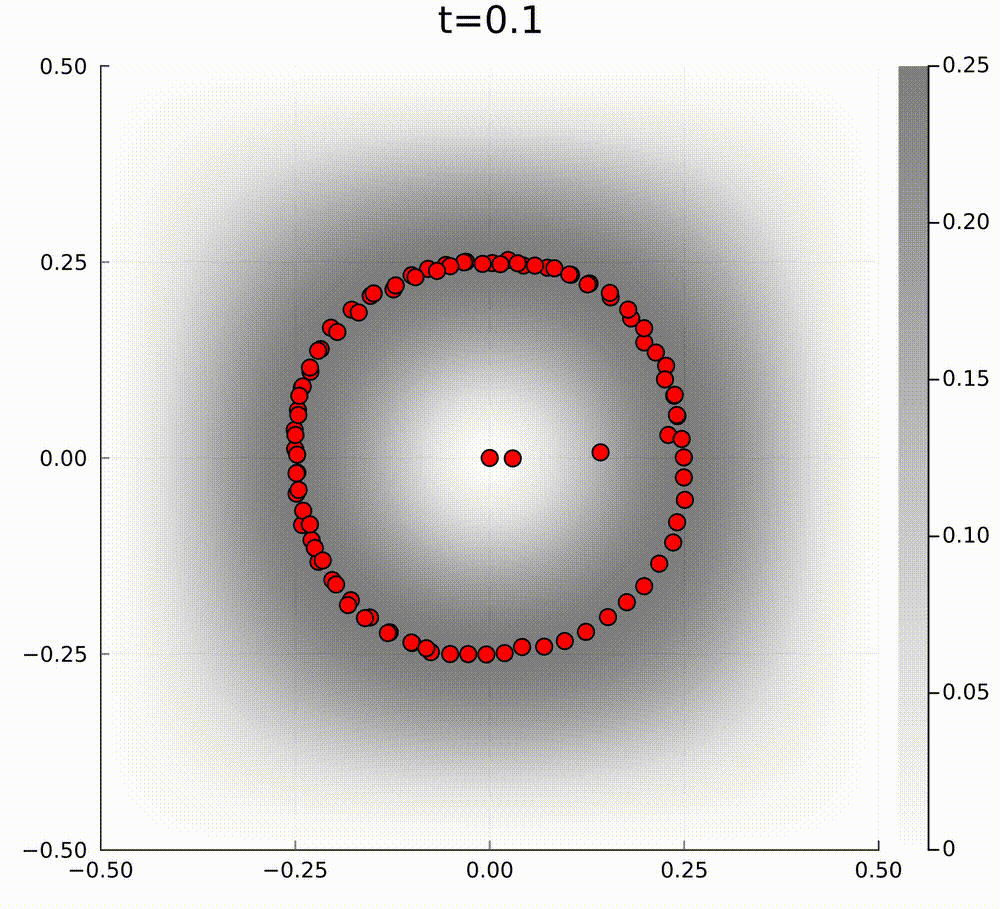
In general, I am interested in studying these type of active matter models to understand emergent collective behaviours.